Theory predicts that it should be possible to violate the second law of thermodynaics. An experiment was constructed to evaluate the theory, and it was found to produce power in the form of electricity from the kinetic energy of molecules of air at room temperature. The experimental power produced by the device over a temperature range of 20 - 55 C was within 5% of that which the theory predicted across the entire range.

Other sources of the power, such as electrochemical were evaluated and eliminated as possibilites.

The Second Law

The second law of thermodynamics is considered by most physicists to be indisputable. The saying goes that if a theory violates this law, then the theory must be wrong. This is despite the fact that the law with respect to entropy can be proven mathematically false (1), and the temperature gradient of the any planet's atmosphere proves it physically false (2) as well. The real question is if it can be experimentally proven false in a laboratory at the macro level on a time scale that humans are comfortable with, something more than microseconds, and less than the age of the universe. If experiments are done and they dispute the theory at macroscopic levels with times of seconds, minutes and hours, then the second law must be declared false, both from a mathematical standpoint as well as a physical reality. There is indeed evidence that for submicroscopic particles this law can be violated. See Beads of doubt (3) for information on this. Even mesoscopic systems can routinely violate the second law as well (4). The reality that it can be violated consistently and continuously at the macroscopic level should show that the concept of the second law of thermodynamics is flawed and false.

"The second law of thermodynamics says that a closed system's entropy can only stay the same or increase, it can never decrease (5). This is of course false for an ergodic function such as entropy as proven by the above reference.

The law can also be expressed as "It is impossible to construct a heat engine that, operating in a cycle, produces no effect other than the ahsorption of thermal energy from a reservoir and the performance of an equal amount of work." (6)

"it is impossible to construct a cyclical machine that produces no other effect than to transfer heat continuously from one body to another body at a higher temperature." (6)

That those last two reference restrict the second law to a machine that is operating in a cycle is curious, generally there is no such restriction on what machines to which the second law of thermodynamics applies. The violation of the second law of thermdynamics outlined in this paper is done though with a device which is NOT cyclic, but rather continuous.

Maxwell's Demon

Maxwell's Demon is a thought experiment which has a door that is opened and shut when a molecule of gas approaches. It is opened if the molecule has greater than the average speed, and closed if it has less. Thus only the "hotter" molecules pass though the door, so the gas on the other side of the door will be warmer than those left behind. This would violate the second law of thermodynamics, and the theory is that the amount of energy required to make the decision on whether to open the door or not equals or exceeds the energy gained by doing so.

Another demon that is closely related is the pressure demon, also known as Maxwell's pressure demon. In this thought experiment the wall acts like a diode, letting molecules of a gas travel in one direction, but blocks them from going the other direction. Thus one side gets pressurized and hot, and the other side loses pressure and gets cooler.

But as the above references indicate, for molecular sized particles and smaller, the second law can be violated. So, does Maxwell's (Pressure) demon provide a way to do this at the macro level? It certainly appears that it might.

Exploring Maxwell's demon, the idea was that one does not want to extract any energy as heat. First this is a low grade energy, and second, it is hard to measure minute temperature differences. It would be much better if we could extract electricity directly. This is easy to measure and quantify. So, if we can construct the door to not let through a molecule, but rather let through an electron from the molecule's shell instead, we would have a method of generating electric current.

Collision Induced Tunneling

As it turns out, this is not difficult to do. The method to accomplish this is called tunneling (see Intro to Quantum Mechanics (7)), a concept that is well understood and quantified in quantum mechanics. Basically an electron has a finite probability of being anywhere within an area around an atom according to Schrödinger’s wave equations. If the molecule is moving, this area increases in size. The average velocity of an oxygen atom at 300 K is just under 500 m/s. So if a molecule of gas hits a few atom thin non-conductor with a conductor behind it, there is a small probability that one of the atom's electrons will tunnel through the insulating layer, and end up trapped on the conductor side. This process is also enhanced by what is termed "collision induced tunneling", which generates a force on the orbital electrons equivalent to a field gradient of over 5 million volts per inch when it is decelerated from the average velocity of a gas particle over the distance of a typical atom. This force is far in excess of what is needed to cause heavy asymmetric tunneling through the insulating layer. This thus becomes the equivalent of Maxwell's pressure demon with the electron.

Thus if we take a sheet of metal, and put a very thin insulating layer on the surface of this, and place another piece of metal next to it with a small air gap between them, we would expect a potential difference to develop between the two sheets. Since electrons would be trapped in the one that has the insulating layer, it should become more negative than the one without the insulating layer, which would continually bleed off any charge by contact with molecules of the air (especially any of which had recently lost an electron).

Putting a thin layer of insulator on a sheet of metal only a couple of atoms thick is usually not easy, except with aluminum. Aluminum will acquire an atom or two thick layer of Aluminum Oxide (Al2O3) on it's surface within seconds of being exposed to any oxygen. So ordinary aluminum will have what is termed a passivated layer on it. This meets the requirements for the Maxwell pressure demon quite well, providing a very thin layer that electrons can tunnel through, yet end up trapped on the aluminum side.

So all that is needed to try this experiment is a sheet of aluminum with a thin sheet of another metal, such as copper or brass, separated by a very small gap. Then a multimeter can be used to measure the potential difference between the two sheets of metal.

Note however that very thin aluminum foil should not work quite as well as a thicker sheet. If the foil is too thin, then the electron can tunnel right through the foil ( http://www.physlink.com/Education/AskExperts/ae619.cfm (8)) and end up on the other side of the foil, instead of depositing a charge on the foil as desired. The aluminum should be at least as thick as heavy duty Reynolds wrap, or the voltage and current developed will be lower than it would otherwise.

With two different metals however, one might surmise that the effect is some type of battery effect. Although there is no known mechanism for this to occur with only air or an insulator between the sheets, the fact that if the aluminum is thin foil the effect should be reduced can be used to disprove this theory. In addition, one could use two different thicknesses of aluminum, and the thinner one should always be positive to the thicker one if electron tunneling is causing the potential difference. Increasing temperature should cause absorbed water to evaporate, and the surface conductivity of the insulator to decrease, thus reducing the power generated by the device, but tunneling will increase and should cause a dramatic increase of power, approximately doubling for every 14 degrees Celsius. Although humidity should increase the power if from chemical reactions, it is likely to increase as well if due to tunneling. From the tests shown below, that the energy is being generated from tunneling of electrons from the captured gas are supported by experimental evidence and is not a chemical reaction except at high humidity levels or wide gaps.

Of course if we are violating the second law of thermodynamics without violating the law of conservation of energy, there must also be a cooling effect on the gas. If we examine a molecule that has collided with the insulating layer and lost an electron, it will bounce off the layer elastically, and move toward the other sheet of metal. However since it has lost an electron, it will be positively charged and slowed by the electric field between the two sheets, so that when it reaches the other sheet and gets neutralized, it has lost the same amount of energy as was deposited electrically on the insulated sheet. Thus this is indeed an implementation of Maxwell's demon. This also puts an upper limit on the voltage that can be developed between the plates. Basically the maximum voltage that can be developed in a rarefied gas will be the kinetic eV times the number of degrees of freedom of the molecule of gas at that temperature. (At 300K or room temperature that works out to be about 116 meV, assuming 3 degrees of freedom. The Diatomic gases nitrogen and oxygen have 5 degrees, but 2 of them are for rotation so should have no effect with an electric field). If the gas is not rarified, then collisions with other molecules can continue to add energy as it loses it by moving toward the other plate so that a voltage can be reached that is significantly higher than the kinetic eV of the gas. The mean free path of an oxygen molecule in air is about 67 nm. Thus for a molecule that has lost an electron to make it back to the copper plate it will encounter d/67 nm collisions on the average with other molecules. For a typical fiberglass screen (d = .01") this works out to be about 240,000nm/67collisions/nm = 3600 collisions. Since collisions will cause the average velocity of a molecule to approach 0, they will tend to cause the molecule to tend to drift back toward the aluminum plate due to the electric field. The result is that the expected energy produced should decrease dramatically as the distance between the plates is increased, and even with this narrow gap, the expected efficiency should be very low. If the energy source is electrochemical then the produced power should not be affected significantly by the distance between the plates. Once again, experimental evidence supports that the energy is from the kinetic energy of the gas molecules and not electrochemical since slight variations in the distance between the plates produce large changes in the voltage.

Temperature Dependence of Tunneling

At any rate the hotter the air between the plates, the higher the voltage that can be developed due to the increased energy of the molecules and increased mean free path. The increased collision rate should also increase the maximum current the device can deliver as well. The other limiting factor is that the gas molecule must have sufficient energy to cause the electron to tunnel through the barrier plus the voltage on the aluminum plate. An air molecule at 300 K will have an average kinetic energy normal to a plate of 38.7 meV at 300 K. A one oxygen thick aluminum oxide potential barrier is reported to have a breakdown voltage of approximately 1.5 volts. Thus the maximum voltage that can be expected to be maintained on the aluminum plate at any temperature cannot exceed this, since at voltages greater than this, a reverse current can develop and discharge the plate. However electrons can penetrate this barrier from gas if it is one or two molecules thick by tunneling.

It is expected that the voltage and current will increase exponentially with temperature. This is characteristic of tunneling, where only the highest energy electrons are capable of tunneling through the barrier. Also it is expected that the effect will be very strongly dependent on humidity. Water has a molecular weight of 18 and can disassociate into a H+ and a OH-. The OH- not only has an extra electron making it negatively charged, but it has a molecular weight of 17, about half of a typical molecule of nitrogen or oxygen in air. Thus a water molecule or hydroxyl radical will be traveling at a velocity approximately 40% faster than that of a typical molecule, approximating a molecule of air at about twice the absolute temperature (600 K or about 330 C). It is expected that at normal humidity levels, the water molecule and hydroxyl radicals will be the primary source of electrons to cross the barrier at temperatures around 300K due to it's higher velocity and negative charge in the case of they hydroxyl radical.

The equation for tunneling through a thin insulating layer is:

I(T) = I(To) * [T/To]^2 * Exp[ - E/2k * (1/T - 1/To) ] (#1)

With a Taylor expansion in the limit of small temperature changes, one can show that the temperature dependence is:

I(T) = I(To) * Exp[a * (T - To)] (#2)

which shows that the expected curve over a limited temperature range is an exponential as we assumed earlier.

See Leakage Current Subtraction and Signal Calibration (9) and The Diode (10)

E is the band gap of the material. The band gap of thick layers of aluminum oxide is approximvately 9 eV. Thin layers, such as one or two atoms thick get into the area of a "size dependent band gap", which will be approximately half of the bulk band gap for very thin films. Thus in the math below I will use a band gap energy of 4.5 eV. A slight error in this number changes the result significantly, so if we get close to the correct answer it should be supportive of the theory.

If we assume we are working with a solid instead of a gas for the electron source, and using 20 degrees C (293 K) as To, then substituting in the above equation #1 we get:

I(T) = I(To) * [T/293]^2 * Exp[ - 4.5/(2*8.6*10^-5) * (1/T - 1/293) ]

Now, if we assume that we are getting tunneling from the collision induced tunneling on one side of the aluminum oxide layer only, then we have either 5 or 6 degrees of freedom for a diatomic and triatomic molecules. For a diatomic molecule this is from 3 translational degrees of freedom, 2 rotational degrees of freedom, and one vibrational degree of freedom. Note that although the vibrational degree of freedom normally adds 2 degrees of freedom, the kinetic and the potential, only the kinetic affects the collision induced tunneling. Some diatomic molucles do not have a vibrational mode, (11) due to their tight binding, such as oxygen and nitrogen. For triatomic molecules there are 3 degrees of translational freedom, and three degrees of rotational freedom, but due to the strong binding for molecules such as carbon dioxide and ozone, there is no vibrational mode. Since there are molecules with both 5 and 6 degrees of freedom, due to the exponential nature of the equation, those with 6 degrees will have much more effect than those with 5 degrees of freedom. Thus we use use 6 degrees of freedom in our computations despite that only a small portion of normal air will be composed of molecules with this many degrees of freedom.. The result is:

I(T) = I(To) * [T/293]^2 * Exp[ - 4.5/(2*6*8.6*10^-5) * (1/T - 1/293) ]

Now, that would be for contant volume, but we used constant pressure, so using Boyles law we compute that the gas density is proportional to 293/T for each measurement:

I(T) = I(To) * 293/T * [T/293]^2 * Exp[ - 4.5/(2*6*8.6*10^-5) * (1/T - 1/293) ]

I(T) = I(To) * T/293 * Exp[ - 4.5/(2*6*8.6*10^-5) * (1/T - 1/293) ]

I(T) = I(To) * T/293 * Exp[ - 4360.5 * (1/T - 1/293) ]

Experimental Verification

A unit was built by putting a sheet of copper between two fiberglass screens then that was sandwiched between two 5X5 inch 1/4 inch thick aluminum plates. This was bolted together with bolts on opposite corners of the assembly. The voltage was measured using a CSi/Speco DMR-2322A with 1 Megohm input impedance on the 200 mV scale (Spec says it is 2 Meg. but is wrong). An Omitron E5CS thermocouple temperature monitor and controller was used to measure temperature. A Maytag kitchen oven with mechanical thermostat was used for the heating.

The white alligator clip is on the thermocouple probe that is inserted into the assembly for recording the temperature.

It was found that the voltage generated was very dependent on the pressure applied to the plates. It was found that as you increased pressure the voltage would peak, then begin dropping off again. Apparently what happens is that the plates are brought closer together so that the air gap decreases until everything is totally flat. After that the screen begins compressing, reducing the cell openings, so the space with air in it decreases. If the voltage were strictly electrochemical, then it would be expected that the voltage would continue increasing, even as the screen got pressed down.

The first test run was to determine if the voltage generated could be electrochemical. Initially the unit was tested at about 30% humidity. The unit was not tightened down at all, just assembled, so that it would be easy to diffuse humid air into the gap. The voltage recorded was 3 mV and the resistance was measured to be 200 Meg ohm. Using a DVM with a 1 Meg input impedance, the initial locomotive force needed if this was electrochemical would be 3X10-3*200X10^6/1X10^6 or about .6 volts. This is an indication that the voltage source could be electrochemical, since the voltage generated electrochemically between the copper and the aluminum tested in water is approximately .66 volts. Then the unit was placed into a sealed container with a wet paper towel and left to sit. Within a few hours the humidity approached 100%. The voltage and resistance was taken again. The voltage had increased to .215 volts and the resistance had dropped to just under 2 megohm. Using these measurements with the DVM impedance gives that the initial electromotive force if from an electrochemical cell of approximately .6 volts again, which is what would be expected if this were being generated electrochemically. These initial tests indicate that at room temperature and when not tightened down the source may be electrochemical. All additional tests have been run at humidity levels under 30% to try and alleviate this possible source of error as much as possible. The hope is that the low humidity reading is apparently from the electrochemical contribution because of the wide gap from not tightening it down since it is known that when tightened down the voltage will approximately double, but the electrochemical voltage should not change.

Since elevated humidity creates an electrochemical cell, testing with varying humidities to confirm if water vapor is or is not a major contributor to the tunneling when using copper sheet and aluminum plates are used is not possible.

Temperature Testing

The bolts on the assembly were tightened from the above measurements until a peak voltage was found, and then left there for the temperature tests.

The following data was recorded

Temperature Celsius	mV potential	Expected mV potential
20	5.7	5.7
25	7.4	7.44
30	9.3	9.63
35	12	12.37
40	15	15.7137
45	19.1	19.93
50	24.6	25.03
55	32	31.23

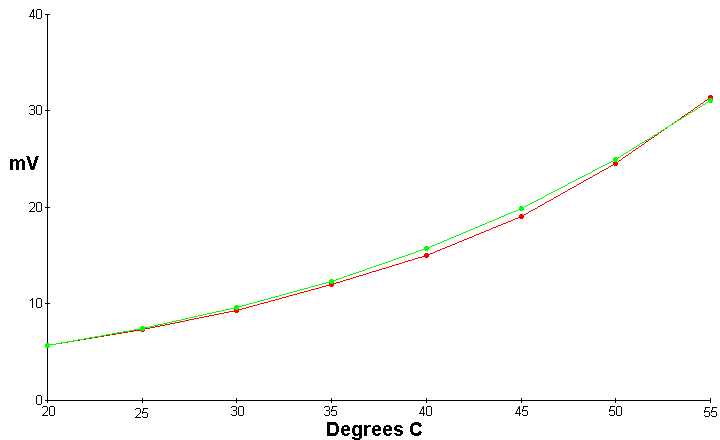
This graph depicts a Maxwell Demon unit which measures 5X5 inches and is a sandwich of copper foil in the center, with fiberglass screen on each side of the foil, and 1/4 inch aluminum plate on each side. This is bolted together and pressure adjusted for maximum output voltage at 20 C and low humidity

The red line is the experimental data, and the green line is a graph of the computed data from the above equations for tunneling from gas molecules. As can be seen the deviation from the expected by the experimental results is never more than 5%.

If the energy were being generated electrochemically from moisture absorbed on the screen creating a battery effect, the voltage and current should drop off with elevated temperatures which would drive off the absorbed layer of water thus discounting that mechanism.

Additional testing using a thick aluminum plate covered with thin aluminum foil and with thin aluminum foil in place of the copper foil has generated up to .5 mV potential depending on temperature, with the thick aluminum plate negative as expected. Since only electrons that not only tunnel through the aluminum oxide barrier but also the entire foil will register in this test, the very low readings are expected and confirm our hypothesis. In this case all electrochemical sources of the potential have been totally eliminated, the same foil is used on both sides of the screen, only the two outside foils are backed by the aluminum plates so that any electrons that tunnel through the foil will still be captured. Tests with elevated temperatures show an exponential increase in voltage and current, which is consistent with the previous measurements. Note that the DVM used had a resolution of .1 mV, so any readings that are half the resolution were bouncing between the two readings. However even with this crude resolution, it is easy to see that the increase in voltage and current is roughly an exponential again as expected.

Data for thin aluminum foil in place of the copper foil, and covering the aluminum plates:

Temperature Celsius	mV potential
20	0.0
25	0.0
30	0.05
35	0.1
40	0.1
45	0.2
50	0.25
55	0.3
60	0.4
65	0.5

The experiment was evaluated for thermoelectric components. For the aluminum foil with aluminum experiment, all thermoelectric components should cancel out, since the same metals at the same temperature are used on both the positive and negative leads. In the case of copper foil in the middle, there could be some thermocouple voltages generated, but these should cancel out as well since the leads were run out of the oven together, and the only thermal drop is where the leads exit the oven, and both leads are identical and of the same material. All junctions are either at room temperature or test temperature, and since the lead material on both is the same, all junction offsets have to cancel out as well.

Humidity Testing of foil and Foil on Plate

Since there is no electrochemical contribution to the aluminum foil vs foil on plate, a humidity test was run once again. The method was the same as before, a wet paper towel was enclosed with the unit and left for several hours. Initially with the humidity under 30%, the voltage measured was 0.0 mV, meaning it was less than 0.1 mV. After being exposed to > 90% humidity for several hours it read 0.3 mV, thus supporting the hypothesis that water molecules are much more efficient at supporting Maxwell tunneling than the gas molecules in air. The potential increased 3 or 4 to one, which is what would be expected if there was a linear relationship between humidity and voltage due to water molecules providing the voltage.

Hydroxyl Testing of foil and Foil on Plate

The device was allowed to stabilize again under 30% humidity. Then it was placed into an enclosure which was infused with ozone. Ozone will react with the humidity present and will produce hydroxyl radicals. This was left for about an hour so it could diffuse into the device and the voltage was measured again. It was found that the voltage increased from <0.01 mV to 2.1 mV. This is a strong indication that either the hydroxyl radical is even more efficient at Maxwell tunneling than a water molecule as expected, or that ozone contributes more tunneling than the normal mix of molecules in air that have 6 degrees of freedom since oxygen and nitrogen only have 5 degrees.

Efficiency

The number of molecules that will be striking the surface of the metal at 300 K can be figured from the equation Molecules/sec/cm^2 = 2.67X10^25/sqrt(MT) where M is the molecular weight of the gas and T is the temperature in Kelvin at atomspheric pressure. This works out to be 2.91X10^23 per cm^2 for nitrogen. A 5 X 5 inch surface is 161.29 cm^2, so with two sides this is 322.6 cm^2. Thus the number of molecules striking both sides of the center sheet is about 9.4X10^25 per second. The current is 1.6X10^19*.0057/1,000,000 = 9.12X10^10 electrons per second. So the efficiency of this is extremely low, with only about one molecule in every 1.03X10^15 producing an electron in the aluminum plate. However, if the hydroxyl radicals are the primary source of the current, then since they only compose about .05 parts per trillion in the air, the efficiency for hydroxyl radicals is approximately 1.9%. Note that since the number of molecules striking the surface per second decreases with the square root of the temperature, and the power produced increases exponentially, the efficiency increases very rapidly with temperature.

Summary

Quantum mechanics provides an easy way to implement a version of Maxwell's pressure demon that produces electricity directly. This violation of the second law of thermodynamics means that there are possibly ways to extract useful quantities of energy directly from the thermal energy of a gas at room temperature. This may at some future date lead to devices that can operate on the temperature of the environment directly. Such devices should no longer be dismissed out of hand as impossible simply because they violate the second law of thermodynamics.

References